Большинство материальных процессов и физических систем являются нелинейными и нестационарными. Это относится и к естественным шумовым процессам, сопровождающим регистрацию какой-либо полезной информации, и к шумам самой измерительной аппаратуры, и к шумам передачи данных по каналам связи. Необходимое условие анализа нелинейных и нестационарных данных заключается в том, чтобы иметь возможность формирования адаптивного базиса разложения сигналов, функционально зависимого от содержания самих данных. Такой подход и реализуется в эмпирическом методе декомпозиции (EMD) преобразования Гильберта-Хуанга (Hilbert-Huang transform, HHT).
Метод EMD основан на предположении, что любые данные состоят из различных колебательных процессов. Каждый режим, линейный или нелинейный, стационарный или нестационарный, представляет простое колебание с нулевым средним значением, в общем случае нестационарное по амплитуде и частоте. Эмпирическая модовая декомпозиция позволяет разложить сигнал на сумму простых взаимно ортогональных колебаний, каждое из которых отображает определенный физический процесс.
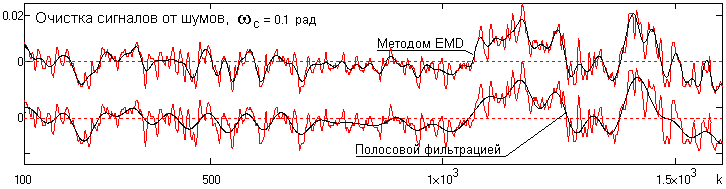
Шумы, сопровождающие полезную информацию в сигнале, в принципе, не относятся к типу колебательных в прямом смысле этого понятия. Но в то же время они полностью удовлетворяют определению простых колебаний с нулевым средним значением по всему частотному диапазону задания сигнала. Это позволяет применить метод EMD для очистки сигналов от шумов. Метод эмпирической модовой декомпозиции обеспечивает более высокую разрешающую способность очищенного сигнала, причем устойчивость очистки, в отличие от частотной фильтрации, сохраняется при достаточно большом изменении частотного порога отсева шумов. Это определяется тем, что при отборе шумов процесс EMD, протекающий в координатном пространстве, в большей степени учитывает динамику локальных неоднородностей распределения отсчетов (локальную статистику отсчетов), в отличие от частотной фильтрации.